Categoria: Uncategorized

Ecco il mio nuovo canale YouTube:

https://www.youtube.com/channel/UC2hubmAOviNnK23mofDUiBQ

L’articolo “Quanto è difficile fare 6 al Superenalotto?” è stato pubblicato sul numero 4/2019 della rivista “Archimede”.

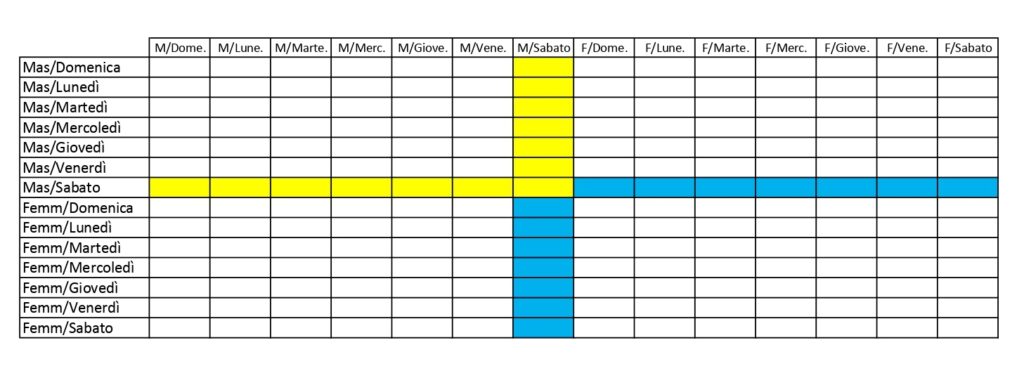
Una donna ha due figli. Almeno uno dei due è un maschio, nato di sabato. Qual è la probabilità che i due figli siano maschi?

(Attenzione, il risultato è del tutto inaspettato!)

• 

Concorso

Articolo sul lancio dei dadi

Questo articolo è stato pubblicato sulla rivista “Giornale Euclide-Scuola” (ISSN 2282-1287) nel n. 54/2019.

Ariete. Siete molto scettici. È per questo che comprerete due conigli per vedere se la successione di Fibonacci è corretta.

Toro. Siete testardi. Avete trovato una dimostrazione della Congettura di Goldbach e siete convinti che sia giusta. Ripensateci.

Gemelli. Siete un po’ sbadati. Nel nuovo anno cercate di non dimenticare più il doppio prodotto… Continuerete, inspiegabilmente, a dimenticarvi dell’esistenza numeri primi gemelli. Fate attenzione.

Cancro. Avete una tenacia fuori del comune, ma continuerete ancora a cercare la quadratura del cerchio. Testardi.

Leone. Sarete affamati, come al solito. Ma dovete ricordare sempre che il Teorema di Pappo-Guldino non è roba da mangiare.

Vergine. Punterete ancora troppo sulla precisione. All’esame vi chiederanno la teoria degli errori. La vostra calcolatrice si scaricherà proprio durante un esame. Portatevi dietro una batteria di scorta.

Bilancia. Puntate sempre sull’equilibrio. Il vostro esame verterà sulla statica dei corpi rigidi.

Scorpione. Al vostro segno è sempre associato il mistero e la segretezza. La crittografia è il vostro approdo naturale, specializzatevi in quel campo.

Sagittario. La fantasia vi potrebbe essere molto utile in ambito matematico, ma avete preferito un posto fisso (??) in banca.

Capricorno. Siete molto ambiziosi, ma lasciate perdere la Congettura di Riemann. A soli 8 anni Gauss sommò i primi 100 numeri a mente. Ma voi abitate in una frazione di Potenza e non temete confronti.

Acquario. L’amicizia per voi è molto importante. Ripassatevi per bene i numeri “amicabili”: ve li chiederanno all’orale.

Pesci. Forse imparerete a nuotare. All’esame vi chiederanno il principio di Archimede. Avrete qualche grattacapo con il “Teorema di Rouché-Capelli” e quindi penserete ad un trattamento anticaduta, a base di omega 3.

Vengono estratti, uno dopo l’altro, i numeri da un sacchetto che ne contiene 90. Qual è la probabilità che, affinché io riesca a completare la mia cartella da 15, sia necessario estrarre tutti e 90 i numeri?

L’animazione fa capire come costruire un ellissografo di Van Schooten (matematico olandese del XVII secolo).

Una proprietà caratterizzante la curva “asteroide” (o “astroide”), definita come x=a*cos^3(t), y=a*sin^3(t): gli assi cartesiani staccano un segmento AB di lunghezza costante (=a) sulla retta tangente nel generico punto P della curva. In figura è rappresentato solo l’arco nel primo quadrante (0 < t < pi/2).

Augusto lancia 80 volte una moneta bilanciata mentre Brunella ne lancia un’altra (anch’essa bilanciata) 81 volte. Qual è la probabilità che Brunella ottenga più teste di Augusto?

Torna alla home page